Initial Controller Design

Overview

Before adding the controller to the onboard software, I had to design it in simulation. Fortunately, I had now an approximate model to use for design. In this post, I'll go over the process of designing a model-based controller in simulation.

Constraints

Since I'll be designing this control in simulation but planning to use it on an actual system, there are a few things that the simulation won't show me that I need to keep in mind. The first of these is the actual limitation of my actuation. My servos are real objects and therefore have limited range, speed, and acceleration. I've documented the expected range of the servos on my aircraft. Dealing with speed and acceleration is more difficult. Unfortunately, I cannot find the datasheets for the servos I'm using. Even if I did, the acceleration, in particular, would change in flight due to the aerodynamic load. To solve this, I am going to find the max speed from a weaker servo that I can find the datasheet for and use its limitation as a conservative estimate for my own servo. Within the simulation, I will cap the servo's output speed to this max speed so that non-physical servo motion is not simulated.

I initially was using MATLAB's lsim to simulate the motion. However, there is no method to access the control input in a closed-loop system with lsim so I ended up writing my own function to replace lsim with my own functionality.

Expected Perturbations

In order to test the control response, I first need to perturb the system. I would like to perturb the system with realistic forces and torques. This is the same as finding the expected process noise of the system. Fortunately, this is very simple using the same math and code I'd set up previously to generate the parameter estimates.

The estimates were fit to find the best estimate for the equation $y=\Theta x$ for every row of the state space matrix representation where $y$ is 1xn the vector of state derivatives, $\Theta$ is the 1xm parameter vector, $x$ is the mxn state and controls vector, n is the number of data points, and m is the number of parameters. Since $y\neq\Theta x$ for any specific data point, the residual $y-\hat{\Theta} x$ contains the process noise vector for the flight.

The mean and standard deviation of these vectors both interest me. Below are the calculated values after non-physical outliers were removed:

$$ \Delta\dot{u}: \text{Mean}:   0.9327m/s^2    1\sigma:  12.1979  m/s^2 $$

$$ \Delta\dot{v}: \text{Mean}:   -3.6895m/s^2   1\sigma:  13.5130   m/s^2 $$

$$ \Delta\dot{w}: \text{Mean}:   2.4308m/s^2   \text 1\sigma:  30.9169  m/s^2 $$

$$ \Delta\dot{p}: \text{Mean}:   2.3433rad/s^2   \text 1\sigma:   13.1695  rad/s^2$$

$$ \Delta\dot{q}: \text{Mean}:   6.6781 rad/s^2   \text 1\sigma:  35.6544   rad/s^2$$

$$ \Delta\dot{r}: \text{Mean}:   -2.0239rad/s^2   \text 1\sigma:  24.4184   rad/s^2$$

My first reaction to all of these numbers is that they seem very large. Though instantaneous acceleration is a more difficult thing to have a gut feel for than velocity or distance, I'm still surprised that the 1 sigmas for acceleration are over a 1g, 3g for the case of the direction of gravity. The rotation rates also feel very high. 

There are a number of explanations. The first is that I do not have a feel for the forces and torques that foamboard aircraft feels in the sky and so my instinct is incorrect. In addition, the process noise accounts for the differences between the nonlinear truth and linear model, so some of the error could be from the approximation. There also might have been significantly more wind up high than I expected. And of course, there could be a bug in my code.  For now, I will move forward with these values and see what kind of controller it takes to null them out.

Design Choice and Simulated Runs

We will do the initial design by perturbing the initial state vector and examining the controller's response. For initial perturbations, I will use the mean and $1\sigma$ values from the process noise to generate an initial state error using the following equation.

$$ \Delta x_0=(\text{mean}+1\sigma)\times0.1 $$

0.1 is a relatively rough number that I'm using but I don't think it will matter too much because after studying the effects of initial state perturbations, I will move onto constant force perturbations. These should be more accurate anyway.

For the controller itself, I will be starting with an LQR designed state-space controller. This optimal controller works very well for multi-input multi-output models like this one. I will begin by designing in continuous time. Though the actual implementation will be running in discrete time, the 20Hz operating frequency is significantly faster than the modes of the system (see periods for oscillation of modes from the last post), so I believe it is reasonable to design in continuous time without too much adjustment for discrete-time. This is another assumption that I will check the validity of through flights and return to if invalid.

Pitch

The controller I settled on for pitch weighted the velocities v, and w, the same, with the pitch rate being 10x less important and the pitch angle 10x higher. This was all weighted as 500x higher than the control inputs. 

$$Q= 500\times\textbf{diag(}[\  1\  1/100\  1\  10\  ]\textbf{)} $$

$$R= \textbf{diag(}[\  1\  1\  ]\textbf{)} $$

In response to the initial perturbation, $[1.31\  3.33\  5.38\  0]$, the response was as shown below.

Pitch response to initial condition perturbation

As shown, all states are within 10% of their original values after 5 seconds. In addition, the controller and elevator inputs are relatively small. For reference, there are over 80 degrees of deflection available to both the throttle and elevator in both directions.

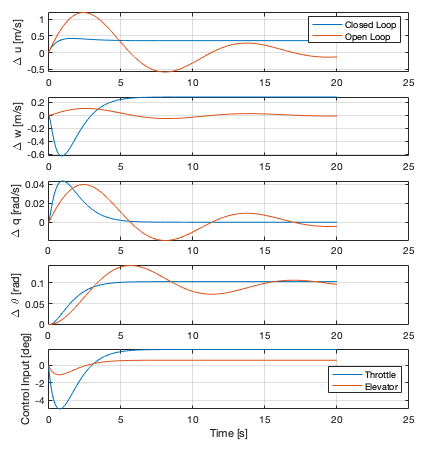
In a slightly more interesting example, the system is given a constant force equal to the bias in the $u$ state. The difference here is that the error is not in the initial condition but instead in a constant acceleration/torque vector applied to the state.

Perturbed with constant force in $u$ direction

The aircraft pitches up and then achieves a new steady-state state and control inputs. You'll also notice an interesting behavior where the Throttle and Elevator work in tandem. Because the throttle pitches the aircraft forward when the throttle increases, the elevator goes up and vice versa.

With some noise added, the results are similar to the above, though no true steady-state is reached due to the constant noise.

Perturbed with constant force and noise in $u$ direction

It is worth noting that even though I've capped the max speed of the servos to a reasonable value, I haven't capped the servo acceleration so it is possible that the quick and fine adjustments aren't possible. There are ways that I can increase the fidelity of this model to truly account for the servo's capability but I believe that this too detailed for this type of simulation and I would rather spend time on other aspects for now.

Roll

I specified the weights for the roll axis very similarly to the pitch axis, with a little bit of extra tuning. I settled on the rotations rates being 100x smaller than the $v$ velocity and the angle $\phi$ being 10x higher. The velocity was also 100x higher weighted than the control inputs. 

$$Q= 100\times\textbf{diag(}[\  1\  1/100\  1/100\  10\  ]\textbf{)} $$

$$R= \textbf{diag(}[\  1\  1\  ]\textbf{)} $$

The response to the initial state perturbation, calculated the same as for pitch, is shown below.

Roll response to the initial state perturbation

All states are nulled to 10% of their max values within 1 second. In addition, the control outputs are both of similar order of magnitude to what we saw in the pitch axis. This is very reasonable and attainable for the physical system.

We can look at a more realistic case by adding both the bias and random noise with the same distribution as found from the residuals. This has the following response.

Here we see that the open-loop angle and velocity arrive at large final offset values but the controller manages to keep both states below 20% of their open-loop error. In addition, we notice that the rates of both open loop and closed loop $r$ and $p$ are very similar. This is a combination of the rotational acceleration being directly connected to the process noise and the controller prioritizing the angle and velocity over angular rates.

Conclusions and Next Steps

I made a lot of approximations in this process and I'm here to defend them. Not because all these approximations were guaranteed to be accurate, but because it is more important to the design process to build it, test it, fly and learn than it is to continue to improve the resolution of this model. My largest assumptions, outside of those made in generating the model, we're assuming the true servo would be capable of similar performance as in the model and that the continuous-time operation would be similar to the onboard discrete-time operation. So if/when this fails in flight, I will look into these two points first.

I am also not entirely convinced that the residual data I pulled to model process noise is entirely accurate. I don't have enough evidence to say otherwise but I will be taking more data in the future to verify and investigate further.

Generally, though, I've learned from and enjoyed this design process. This was the first time I used an actual system's process noise to perturb my simulation model. Though what I've designed may not be the optimal controller in the system level sense, I believe that it's good enough for a first try on the aircraft. I'm sure I will have learned many things by then and look forward to returning to the drawing board with a fresh perspective.